Modified Files:
src/disney_brdf.cpp
src/mesh.cpp
include/mesh.h
Validation Files:
scenes/disney_brdf/chi2test-disneybrdf.xml: the file includes strong chi test adapated from chi test for microfacet brdf in the assignment 3.
scenes/disney_brdf/brdf_env: the folder constains batch validation for different parameters on a simple scene with a sphere, a environmental light and a arealight.
scenes/disney_brdf/area_light: the folder contains a scene rendered with different direct integrator to validate sampling strategy.
scenes/disney_brdf/teapot: the folder constrains a scene with complex mesh shape (e.g. teapot) to verify the robustness of tangent vector computation.
Implementation Details
The implementation is based on the paper Physically Based Shading at Disney published in 2012. The reference code is Walt Disney BRDF Explorer, which can't be compiled.
The five features I implemented are metallic, specular, roughness, anistropic and sheen. The implementation mainly consists of four parts: eval(), pdf(), sample() and tagent vector.
Eval
The disney BRDF follows the routine of microfacet model. The eval() function takes light and view directions and returns the brdf term. The evaluation procedures generally consists of two lobes: diffuse lobe and specular lobe.
Diffuse: the diffuse lobe reflects tinted light and has one fundamental sub-lobe and two plug-in sub-lobes (sheen and subsurface, but subsurface lobe is ignored.) In the fundamental lobe, the tinted reflectance generally follows the diffuse BSDF, the exception is at the grazing angle where 'roughness' parameter controls the response magnitude from 0.5 to 2.5. In the sheen plug-in sub-lobe, the lobe has a high response at the grazing angle where the half vector and view direction (or light direction) have a angle difference near 90 degree. The lobe is linearly controled by 'sheen' parameter and sheen color is the original color (sheenTint=1.0).The response of the whole diffuse lobe is controlled by 'metallic' parameter.
Specular: this lobe has one primary lobe which is implemented and supports metallic and anistropic, and one auxillary clearcoat lobe which is ignored. For the primary lobe, similar to microfacet model, it has shadowing factor(Gs), microfacet distribution(Ds) and Freshnel reflection coefficients(Fs). Fs can be seen at non-linear interpolation between specular relfectance and unity at grazing angle. Gs is modeled by Smith GGX shadowing factor. Ds is modeled by GTR2 model which has longer tail than Beckmann function.
For details, please refer to the paper and source code.
Sampling and PDF
For sampling, I follows the scheme of microfacet bsdf model, which consists of a cosine weighted sampling for diffuse lobe and a GTR sampling for specular lobe. Choosing GTR for sampling is because it has closed form. The cosine weighted sampling is already implemented in the previous assignment. The GTR sampling and pdf is implemented as described in the supplementary materials of this paper. (specifically, the pdf is B.2: Eq.13 and B.1:pdf converion, the sampling is B.2: Eq.14 and Eq.15.)
During the validation, I found that if cosine-based diffuse sampling and specular sampling are combined by exactly '1-metallic' and 'metallic' coefficients, when roughness = 0 and metallic = 0, all the samples will come from cosine-based sampling, but this distribution is quite different from the specular lobe, resulting many white points at the grazing angle (sphere boundary). I squeeze the cosine-based sampling to [0, (1-metallic)/2] and enlarge the GTR sampling respectively. This will enforce the specular lobe is always sampled and better conforms the expected distribution.
Tangent Vector
To support the anistropic style, tagent vector must be continuous over the entire mesh. The methods of making the tagent vectors change smoothly are diverse. I implemented three methods: spherical uv, principle curvature and principle axis (main axis).
Spherical UV: this method has limited application and only works for mesh with convex shape. It firstly represent each vertex with spherical \(\theta, \phi\) coordinate, then the tagent vector is computed by taking the derivative w.r.t \(\theta, \phi\).
$$x = \sin(\theta)\cos(\phi),\ y = \sin(\theta)\sin(\phi),\ z = \cos(\theta)$$
$$t_1 = (\frac{\partial x}{\partial u}, \frac{\partial y}{\partial u}, \frac{\partial z}{\partial u}),\ t_2 = n.cross(t_1)$$
Principle Curvature: the principle curvature function by libigl package computes the continuous tangent vectors which point to the directions of maximum and minimum changing. Though the continuity is preserved, yet the final result is not visually intuitive in our validation.
Principle Axis(main axis): By explicity specifying a main axis, we can easily derive the tagent vector through cross operation. Because the normal direction and cross operation are both continuous, the resulting tagent vectors are continuous.
$$t_1 = n.cross(axis_{main})$$
$$t_2 = n.cross(t_1)$$
Validation
Gradual Change With Parameters

note1: for each row, except the specified parameter, other parameters are fixed. But default values are not consistent among the different rows. For details, please refer scenes/disney_brdf/brdf_env/note.txt.
note2: in metallic row, the environmental lighting is turned down for better comparison.
Sampling and PDF Validation
I perform chi test for three different parameter combinations and pass all the testcases, showing consistency between pdf() and sampling().
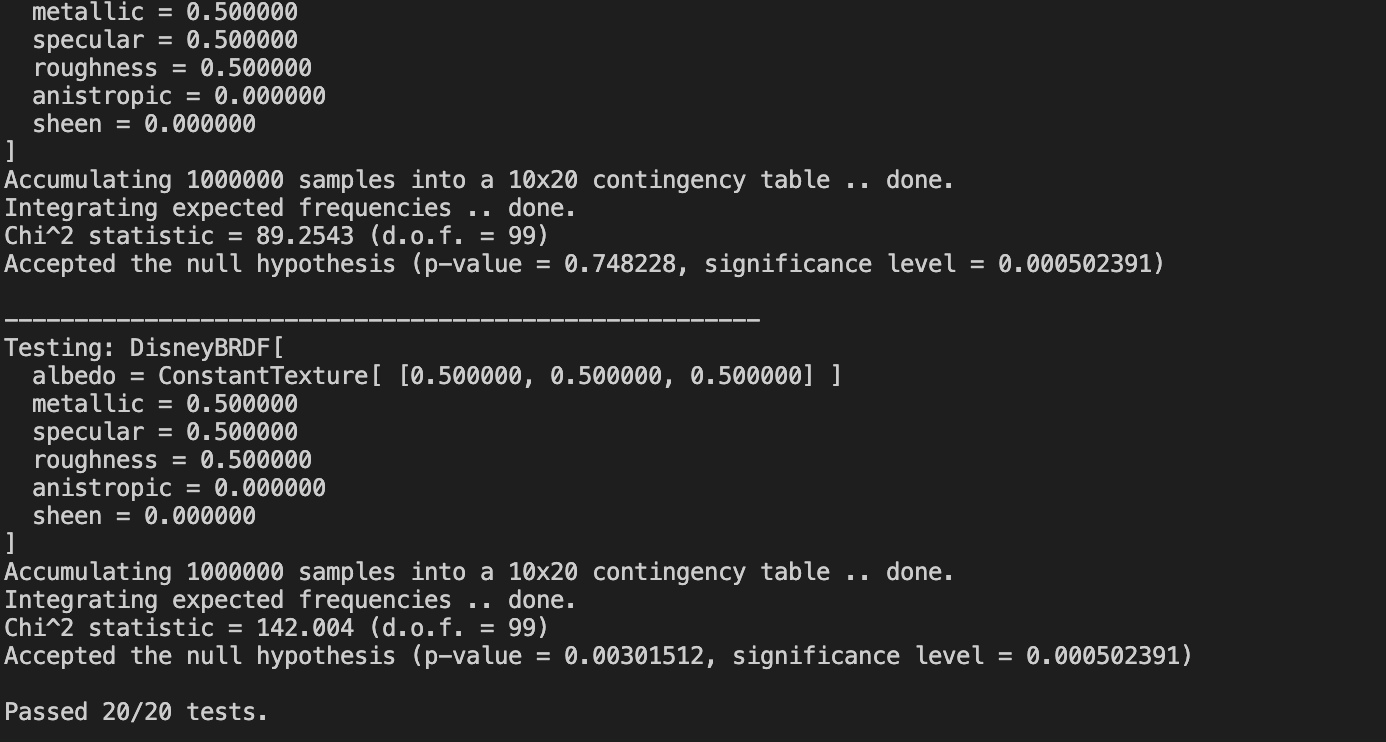
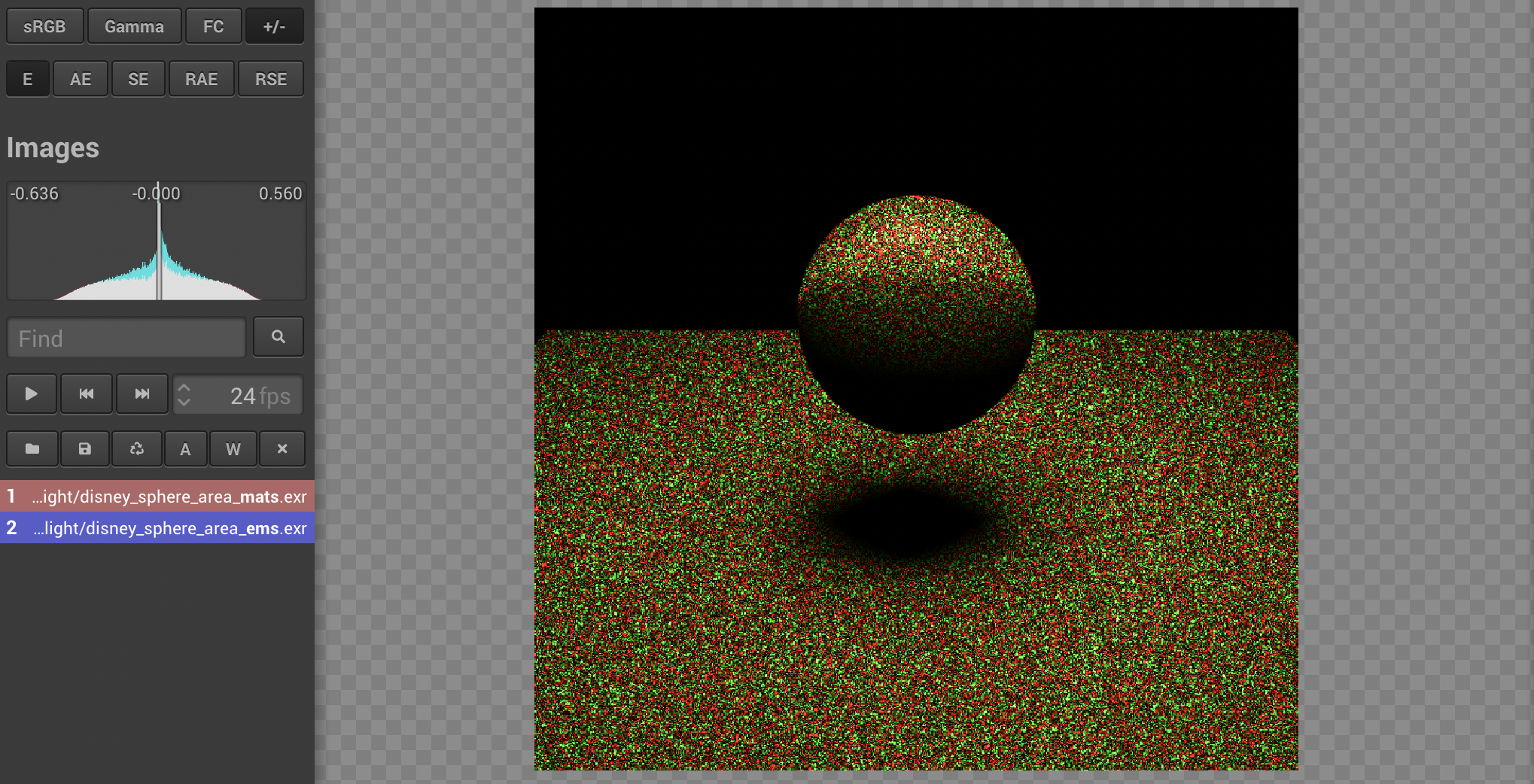
The consistency between pdf() and sampling() could also be validated through comparing rendered images by direct_ems and direct_mats,in which the expected mean error is 0.0.


Anistropic on Complex Mesh
Spherical coordinate-based tagent vector computing works well for sphere mesh, but for more complex mesh (e.g. teapot), the result is not stable. During the validation, I experimented three tagent vector computing methods and find the principle axis (main axis) works the best. Sphereical method not works well because the teapot mesh is complex and non-convex. Principle curvature does not work well because the curvature depicts the shape property but not material property.





